Le temps l'emporte et ne m'en laisse que des lambeaux informes”
Georges Perec
La photo-finish a le pouvoir d'imprimer le mouvement et l'écoulement
du temps sur un espace plat.
Dans son ouvrage The Art of Strip Photography[1], le photographe et
universitaire Maarten Vanvolsem s'intéresse au potentiel narratif des photos-finish, qui peuvent être lues
d'un bout à l'autre du support, tels des rouleaux de peinture sur soie de la Chine
ancienne.
Mais au-delà de l'apport de la photo-finish à l'art et à la
science de capturer le réel en tenant compte de sa dimension
temporelle, ces images ont une beauté intrinsèque, que je qualifierais
de platonicienne, dans la mesure où elles constituent des
empreintes sensibles des lois physiques du mouvement à l'œuvre
dans l'univers.
Cet article est une introduction "artistico-scientifique" à ces empreintes, au langage de la photo-finish, à sa poésie et à ses ambiguités. Il traite essentiellement d'empreintes de mouvements humains, mais aussi de Rubik's cubes et de canards en plastique.
Technique
Paradigme du lire
Typologie du voir
Ambiguïtés du langage : quelques paradoxes amusants (ou inquiétants ?) de la photo-finish
Photos-finish animées
Photo-finish et interprétation artistique
Notes et références
Technique
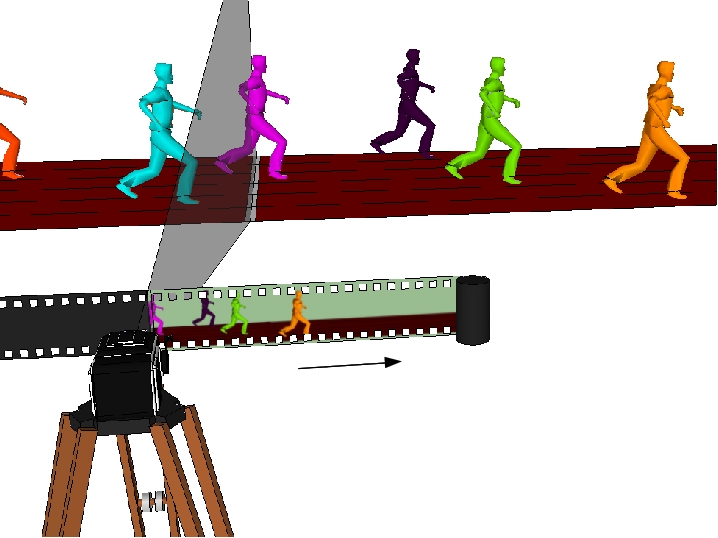La photo-finish a été inventée en 1937 par Lorenzo Del Riccio pour l'ouverture à San Diego de l'hippodrome de Del Mar. Le principe est de faire défiler une pellicule photographique devant une fente d'obturation alignée sur la ligne d'arrivée (voir mon petit schéma ou cette vidéo qui illustre le procédé).
L'image obtenue (la photo-finish) est une succession de bandes fines montrant le même lieu (une zone de faible épaisseur située au-dessus de la ligne d'arrivée) à des instants différents. Si la pellicule a défilé vers la droite, il suffit de lire la photo-finish de droite à gauche pour connaître l'ordre d'arrivée de la course. Mieux encore, si l'on connaît la vitesse de défilement de la pellicule et le point de départ, chaque ligne verticale de la photo-finish peut être associée à un temps de course très précis.
|
Le 1er juillet 1977, l'athlète et championne olympique est-allemande Marlies Göhr devient la première athlète à courir un 100 m en moins de 11 secondes avec chronométrage électronique. La photo-finish de cette course a été conservée et, par la magie d'Internet, est présentée ci-contre[2]. Je me suis amusé à tracer la ligne verticale passant par le buste de la coureuse la plus à droite sur la photo-finish (qui est donc la gagnante de la course, Marlies Göhr) : on peut lire au bas de la pellicule le record historique, 10 s 88.
Des caméras numériques ont aujourd'hui remplacé les pellicules argentiques dans les stades d'athlétisme, mais le principe est resté identique. Plusieurs centaines d'images numériques sont capturées par seconde, et les bandes centrales de ces images (de largeur 1 pixel) sont mises bout-à-bout pour former la photo-finish. C'est de cette manière que je fabrique mes propres photos-finish (j'utilise néanmoins une caméra numérique de bien moindre résolution temporelle et spatiale que celles utilisées dans les stades).
Paradigme du lire
La photo-finish de Marlies Göhr et de ses compétitrices ressemble à s'y méprendre à un instantané de huit coureuses plus ou moins avancées dans leur couloir. Et pourtant, chaque coureuse marque la pellicule de son empreinte au moment même où elle franchit la ligne d'arrivée. Pour l'écrivain et critique Patrice Blouin, il résulte de ce paradoxe un "trouble persistant de la perception", que seul un changement de paradigme permet d'éluder :
|
“Regarder une photo-finish et admettre que chacun des coureurs que je vois réunis dans un même cadre est séparément, dans son couloir, en train de franchir la même ligne d'arrivée, voilà ce qui résiste à l'appréhension. Pour échapper à ce trouble persistant de la perception, je n'ai pas d'autre choix que de changer totalement de posture. (...) Pour une part cruciale de son fonctionnement, une photo-finish se lit, en effet, plus qu'elle ne se voit. Seul ce changement décisif de paradigme permet de s'approprier réellement l'image. Si je veux appréhender une photo-finish, il me faut d'abord la considérer comme un rouleau déplié (et non comme un bloc). Et il me faut en outre renverser mon sens habituel de lecture. Pour déployer ses virtualités empilées, je dois remonter, lentement et progressivement, de droite à gauche, le long de la photographie. Et cette remontée à contre-courant refait alors défiler sous mes yeux, comme par magie, le final de la course. De l'énigme de sa fausse évidence à l'effet fantastique de son redéploiement, en passant par le rituel contre-instinctif (contre-culturel) que réclame son appréhension, tout dans la photo-finish la rapproche d'une production ésotérique et sacrée. Invention de la science du XXe siècle, elle n'existe qu'à l'instar d'antiques formules cabalistiques que l'on doit déchiffrer à l'envers pour qu'advienne le sortilège.”[3] |
Il me plaît de prendre des photos-finish dans la rue ou dans des hyper/supermarchés. Je filme au hasard des petites scènes de vie ordinaire, aussi insignifiantes qu'universelles, parfois comparables à des "spectacles à peine perceptibles" de Georges Brecht. Ce n'est que plus tard, devant l'écran de mon ordinateur, que je découvre avec fascination les images recomposées.
|
|
Demi-tour avec caddie (se lit de droite à gauche) |
|
Ainsi ce Demi-tour avec caddie (par abus de langage et pour reprendre la terminologie argentique, j'appellerai "fente d'obturation" la ligne verticale de largeur 1 pixel située au milieu de l'image vidéo) : une femme s'engage dans une allée de grand magasin en poussant un caddie. Elle traverse la fente d'obturation mais s'arrête avant de l'avoir entièrement dépassée, réalisant sans doute que cette allée ne comporte pas le produit recherché. Elle tire alors le caddie vers elle tout en lui appliquant un mouvement de rotation à 180 degrés afin de ressortir de l'allée. Durant cette habile manœuvre, elle repasse entièrement derrière la fente d'obturation (mais pas le caddie qui reste sous la fente durant tout le temps du demi-tour).
Ces petits événenents étalés dans la durée se retrouvent rassemblés dans une même photo-finish, donnant l'illusion d'une étrange simultanéité dans laquelle trois soeurs jumelles, dont deux siamoises, consultent les produits d'un rayonnage de supermarché.
Typologie du voir
Mais l'attrait exercé par une photo-finish ne réside pas uniquement dans l'énigme de sa lecture ou dans l'étrangeté des figures émergentes. Il réside aussi, je crois, dans la beauté de ses formes. La photo-finish du "demi-tour avec caddie" me fait voir un élégant pas de danse, que rien ne laissait présager dans la vidéo originale. Cette harmonie naturelle, souvent rencontrée dans les photos-finish, a sans nul doute quelque chose à voir avec le principe fondamental de moindre action à l'œuvre dans ces images, et qualifié en son temps par Maupertuis de “sage et digne de l'Être suprême”[4].
Et de même que la perspective centrale possède des propriétés géométriques remarquables (ligne d'horizon, points de fuite etc.), la photo-finish présente une géométrie singulière, fonction de la durée et du mouvement, qu'il est passionnant autant qu'amusant d'explorer. Je tente ici de dégager quelques "archétypes géométriques" ou "formes platoniciennes" fréquemment rencontrés dans les photos-finish. Ces archétypes correspondent à des empreintes bidimensionnelles de mouvements rigides (éventuellement articulés) effectués dans l'espace tridimensionnel.
Afin d'obtenir dans un premier temps des archétypes élémentaires, je me suis intéressé à faire subir des mouvements simples à un rubik's cube virtuel et à calculer les photos-finish de ces mouvements. Pour ne pas trop alourdir cette page, les formes obtenues sont rassemblées dans une fenêtre à part que l'on peut afficher en cliquant ici (certaines de ces formes sont reprises ci-dessous).
Étirement / compression
 |  |
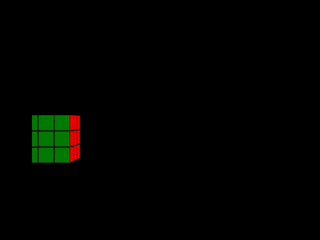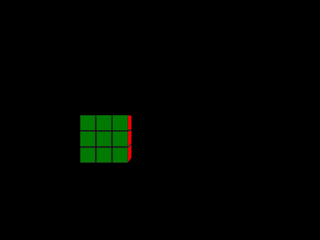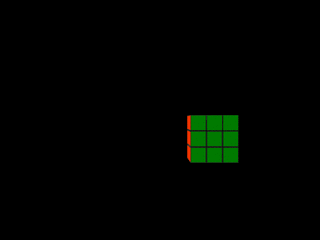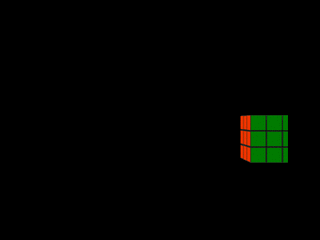| Mouvement latéral | Photo-finish |
 |  |
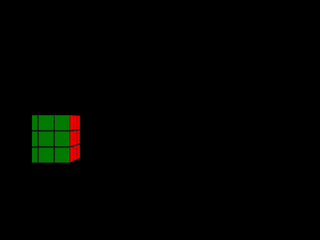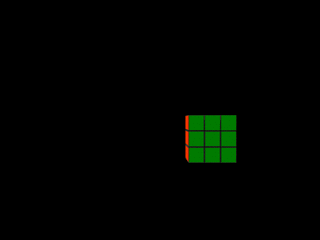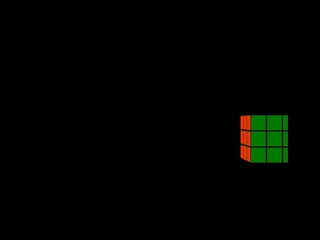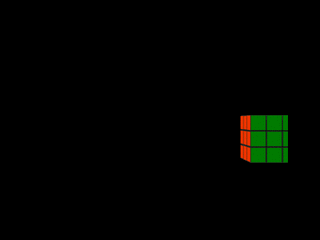| Mouvement latéral plus rapide | Photo-finish |
 |  |
| Mouvement latéral plus lointain | Photo-finish |
Lorsqu'un objet se déplace latéralement derrière la fente d'obturation, son épaisseur dans la photo-finish est fonction de sa vitesse. On peut voir cela dans les deux premières photos-finish synthétiques du rubik's cube (mouvements latéral et mouvement latéral plus rapide). Lorsque le cube traverse la fente d'obturation, des rectangles verts de largeur 1 pixel sont capturés. Plus le cube passe vite, moins le nombre de rectangles acquis est élevé, et plus la forme résultant de leur agrégation est étroite. Le rectangle de la deuxième photo-finish synthétique est ainsi plus fin que celui de la première. Il est aussi légèrement décalé vers la droite car, le cube étant plus rapide dans ce cas, il atteint plus tôt la fente d'obturation (rappelons que le temps croît de droite à gauche sur l'axe horizontal d'une photo-finish).
L'épaisseur d'un objet dans une photo-finish est inversement proportionnelle à sa vitesse lors du passage derrière la fente d'obturation.
Ce principe est à la base de nombreuses distorsions visuelles fréquemment observées dans les photos-finish. Par exemple, lorsque nous faisons un pas en avant, le pied d'appui s'immobilise quelques instants ; cela se traduit dans la photo-finish par une longue trace de chaussure qui remonte aux extrémités en raison du mouvement de tangage exercé par le pied. Cet archétype est récurrent dans les photos-finish de rue, je l'appelle "chaussure de clown". La jambe d'appui suit quant à elle un mouvement pendulaire inversé : rapide (étroit) au sommet et lent (large) à la base, formant grossièrement un triangle pointant vers le haut. Dans certaines configurations, la base de ce triangle se confond avec la chaussure de clown, et lorsque la jambe d'appui occulte la jambe libre, on obtient une sorte de socle sous le tronc de la personne qui ressemble alors à une statuette ou une pièce de jeu d'échec (archétype "piédestal"). La jambe libre opère un mouvement un peu plus complexe : pour simplifier, la cuisse suit un mouvement pendulaire autour du bassin (qui se traduit dans la photo-finish par un triangle pointant vers le bas) et le bas de la jambe un mouvement pendulaire plus ample autour du genou, lui-même en déplacement (qui se traduit par un fin trait vertical). L'association des deux formes ainsi obtenues constitue l'archétype "jambe de bois" ! Ces trois archétypes sont visibles dans la photo-finish ci-dessous ("jambe de bois" et "chaussure de clown" pour l'enfant à l'avant-plan, "piédestal" pour l'homme poussant le caddie).
archétypes "jambe de bois", "chaussure de clown" et "piédestal"
Mobilité / immobilité
 archétype "chenille" |
Si un objet reste immobile dans l'axe de visée de la caméra durant toute la prise de vue, la même bande verticale est dupliquée sur toute la largeur de la photo-finish. Il s'agit du cas limite de la règle précédente (vitesse nulle => largeur infinie). Cela explique les traînées horizontales visibles dans la photo-finish ci-dessus, ainsi que l'impression de voir un rayonnage de supermarché dans la photo-finish du "demi-tour avec caddie". Si l'objet reste immobile pendant un temps limité, la même bande est dupliquée dans la photo-finish sur une largeur égale à la durée de son immobilisation (archétype "chenille").
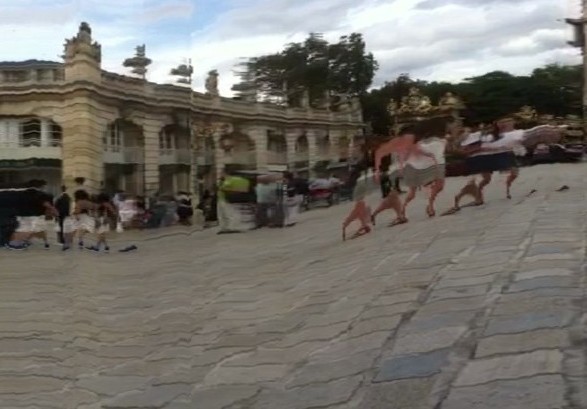Une photo-finish est habituellement obtenue à l'aide d'un appareil
d'acquisition parfaitement immobile, afin d'obtenir des temps de
course extrêmement précis. Le terme strip photography est
parfois utilisé pour désigner l'utilisation de la technique de la photo-finish
en dehors du contexte sportif. Patrice
Blouin propose de traduire ce terme par "photo-frise" ou
"photo-ruban". Une des spécificités de la photo-frise par rapport à
la photo-finish est que l'on s'autorise à bouger la caméra ou
l'appareil photographique au cours de la prise de vue, le chronométrage des événements n'étant plus une finalité. Les objets
immobiles "défilent" alors derrière la fente d'obturation. Ce
mouvement apparent se traduit par une "image scanner" de la
partie immobile de la scène.
Lorsque la caméra suit un mouvement de rotation horizontale à vitesse angulaire constante, on obtient une image panoramique de l'environnement immobile et il devient alors possible de faire cohabiter au sein d'une même image les lois spatiales de la perspective centrale avec les lois temporo-spatiales de la photo-finish.
Profondeur et parallaxe
 |  |
 archétype "queue de paon" |
Une loi bien connue de la perspective centrale est que les objets lointains apparaissent plus petits que les objets proches de même taille. Cette loi explique la forme en "queue de paon" de la photo-finish d'un rubik's cube s'approchant du dispositif d'acquisition avec une vitesse constante dans l'axe de visée. Les courbes obtenues (frontières haute et basse et courbes intérieures) sont des branches d'hyperboles[5] (ces courbes sont légèrement aplaties à leurs extrémités en raison de l'accélération initiale du cube et de sa décélération en fin de trajectoire). On peut observer une telle forme dans la photo-finish ci-contre (l'apparence multicéphale et les ondulations sur le tee-shirt sont dues au déhanchement provoqué par la marche, qui fait tanguer le corps de part et d'autre de la fente d'obturation).
Mais en même temps que les objets rapetissent à mesure qu'ils s'éloignent, leur parallaxe, c'est-à-dire leur vitesse apparente, diminue (par exemple la lune semble ne pas bouger dans le ciel, alors qu'elle parcours plus de 1000 mètres par seconde) : ils apparaissent donc plus larges dans la photo-finish qu'ils ne le seraient s'ils étaient proches. Ainsi, la largeur du rectangle dans la photo-finish du "mouvement latéral plus lointain" du rubik's cube présentée plus haut ne diminue pas en proportion de la hauteur : elle est à peu près identique à la largeur du rectangle correspondant au mouvement proche.
Un mouvement oblique est la combinaison d'un mouvement latéral et d'un mouvement frontal. Les photos-finish obtenues font donc apparaître à la fois l'effet parallaxe et l'effet queue de paon. Ainsi, dans la photo-finish d'une allée de supermarché visible ci-contre, de belles courbes sont obtenues notamment au niveau des ombres, tandis que le caddie est presque aussi large à l'arrière qu'à l'avant, défiant les lois habituelles de la perspective. On peut aussi observer cette combinaison d'effets sur le mouvement oblique de rubik's cube présenté sur la page dédiée aux mouvements de cet objet.
Dépliage
 |  |
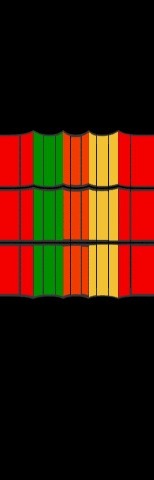 archétype "cubisme" |
Un objet en rotation sur lui-même, ou de manière équivalente, un objet immobile autour duquel on se déplace, se retrouve "déplié" dans la photo-finish. Ce phénomène est comparable à la projection de Mercator d'un globe terrestre. Les effets visuels générés par ce type de mouvements ressemblent aux représentations en points de vue multiples (ou "perspectives mobiles") utilisées dans de nombreuses peintures du mouvement cubiste.
Répétition
Nous avons déjà rencontré ce phénomène, par exemple dans la photo-finish du demi-tour avec caddie : lorsqu'une personne passe plus d'une fois derrière la fente d'obturation, nous obtenons dans la photo-finish un effet d'ubiquité corporelle (archétype "clonage") si la personne passe entièrement derrière la fente, ou des jumeaux, triplés ou plus fusionnés (archétype "frères ou soeurs siamois") si elle passe alternativement de part et d'autre de la fente sans la dépasser complètement. Notons au passage que les archétypes peuvent être combinés, comme pour la "femme multicéphale" qui incarne simultanément l'archétype "queue de paon" et l'archétype "soeurs siamoises".
Ambiguïtés du langage : quelques paradoxes amusants (ou inquiétants ?) de la photo-finish
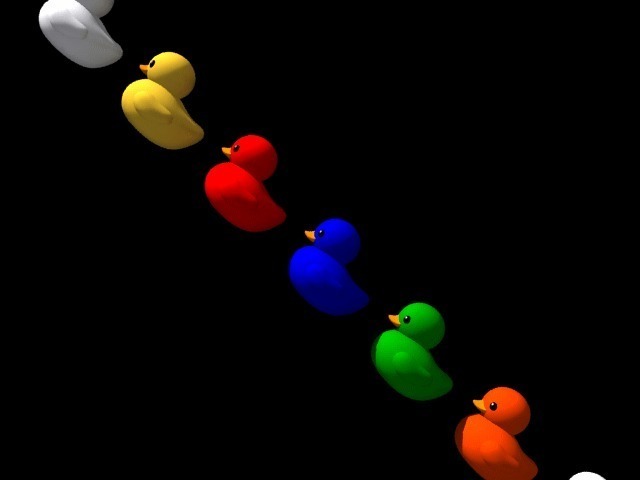
Le monde vu à travers une fente est décidemment fort déroutant ! Je décris ici quelques paradoxes ou "fausses évidences" de la photo-finish. Comme la plupart de ces paradoxes concernent des relations spatio-temporelles entre plusieurs objets en mouvement, j'ai choisi d'utiliser des séries de canards pour les illustrer. Une page est dédiée à ces séries, que l'on peut ouvrir en cliquant ici.
Un sens de circulation que nul ne peut enfreindre
 |  |
 |  |
De l'autre côté du miroir, la symétrie elle-même est chamboulée. Une photo-finish de canard passant derrière la fente d'obturation dans le sens gauche / droite montre un canard orienté vers la droite : rien d'étonnant à cela. Mais qu'en est-il d'une photo-finish de canard passant derrière la fente d'obturation dans le sens opposé, de droite à gauche ? Eh bien elle est identique à la première, le canard a été "retourné" et regarde, comme dans le cas précédent, vers la droite (l'instant 0) de la photo-finish. Pour comprendre cela, il faut s'imaginer une ligne d'arrivée au milieu des images animées présentées ci-contre : le premier canard franchit la ligne de gauche à droite, le second la franchit de droite à gauche. Mais dans les deux cas, le bec du canard passe la ligne d'arrivée avant la queue, et se trouve ainsi plus à droite que la queue (plus en avance) dans la photo-finish. Ainsi,
tous les êtres ou objets traversant la fente d'obturation dans un sens ou dans l'autre semblent avancer dans le même sens, de la gauche vers la droite, dans la photo-finish.
Il est impossible d'échapper à cette règle, fondamentalement liée au fait que l'on avance toujours vers son lieu futur. Il en résulte un (inquiétant ?) effet d'homogénéisation des déplacements (voir toutes les photos-finish de cette page, et en particulier la photo-finish du manège à canards visible ci-dessous), qui fait étonnamment écho à ce passage du roman l'Enquête de Philippe Claudel :
 |  |
| “Un flot humain passait en grand silence à quelques mètres devant lui, sur les trottoirs : une foule dense, rapide, qui filait à toute allure, comme aspirée par un formidable appel d'air. Elle était constituée de femmes et d'hommes de tous âges, mais qui marchaient à la même vitesse, ne se parlaient pas, regardaient soit le sol, soit devant eux. Ce qui était totalement singulier, c'était que, sur le trottoir le plus proche de lui, la Foule allait de la gauche vers la droite, alors que sur l'autre trottoir, de l'autre côté de la chaussée, c'était l'inverse, comme si, quelque part, quelqu'un avait instauré un sens de circulation que personne n'osait enfreindre.”[6] |
L'homme qui tire plus vite que son ombre
 |  |
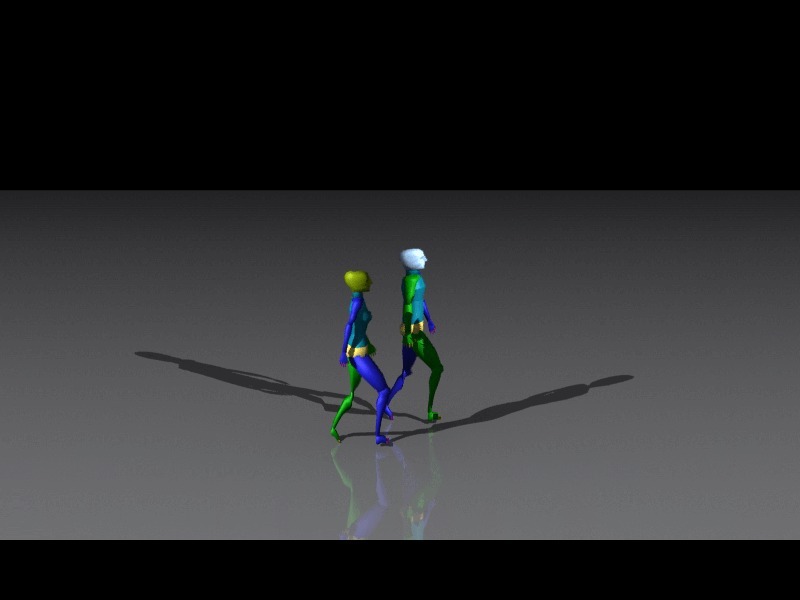A quoi correspondent les ombres d'une photo-finish ? Pour tenter de répondre "scientifiquement" à cette question, j'ai calculé la photo-finish d'une rencontre entre deux bipèdes (objets standards du logiciel 3ds Max). On retrouve tout d'abord le paradoxe précédent : alors que les deux bipèdes se croisent dans l'animation, ils semblent marcher côte à côte dans la photo-finish. Mais ce paradoxe s'applique aussi aux ombres, produisant une image plus saisissante encore car impossible à obtenir habituellement, dans laquelle des ombres sont croisées au lieu d'être alignées ! Les ombres d'une photo-finish ne renseignent donc pas beaucoup sur la position des sources lumineuses, d'autant que leur orientation dépend aussi de leur vitesse de passage derrière la fente d'obturation. En revanche, la même photo-finish sans les ombres ne permettrait pas de savoir si les deux bipèdes marchaient dans le même sens ou en sens contraires lors de leur passage derrière la fente d'obturation. La présence des ombres permet de lever cette ambiguïté : croisées, elles indiquent que les bipèdes marchaient en sens contraire.
Mais le paradoxe des ombres ne se limite pas à l'ambiguïté de symétrie. Si les ombres sont croisées dans notre exemple, c'est parce que le bipède "femme" est précédé par son ombre tandis que le bipède "homme" précède son ombre. La photo-finish du passage de l'ombre derrière la fente d'obturation correspond généralement à une fenêtre temporelle antérieure ou postérieure à celle du passage de l'objet "émetteur" de l'ombre. Nous pouvons clairement le voir dans la photo-finish ci-contre, notamment au niveau de l'ombre des jambes du bipède "homme", qui semblent entrelacées alors qu'elles sont écartées au niveau du bipède sensé émettre l'ombre. Dans ce cas, l'ombre est postérieure au bipède (elle traduit les mouvements du bipède après qu'il soit passé derrière la fente). 
Dans le cas du bipède "femme", l'ombre est antérieure au bipède, c'est-à-dire paradoxalement, en retard par rapport au bipède.
Ainsi, si ce bipède était Lucky Luke, la photo-finish de l'ombre pourrait correspondre au moment où il s'apprête à dégainer, et la photo-finish du bipède au moment (suivant) où il tire, exactement comme dans cette célèbre vignette de "l'homme qui tirait plus vite que son ombre".
Il est à noter enfin que, dans la mesure où le reflet d'un objet sur un plan horizontal correspond exactement à une symétrie verticale de cet objet, les photos-finish des reflets des bipèdes visibles dans nos exemples sont les symétriques (les reflets) des photos-finish des bipèdes qui se reflètent. Cela n'est généralement pas le cas avec des objets réfléchissants plus complexes qu'un plan horizontal.
Ce plat pays qui est le mien
 |  |
 |  |
 |  |
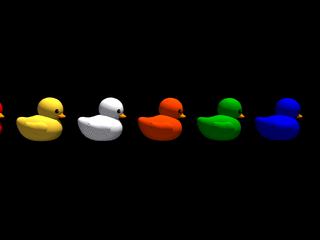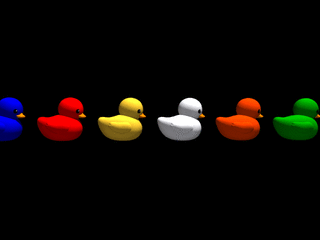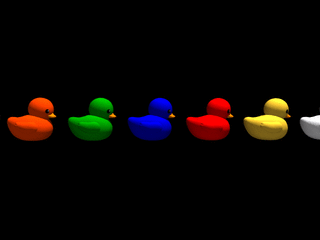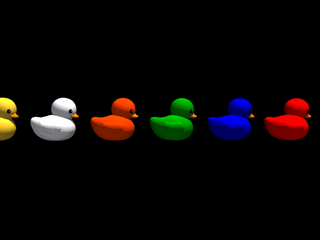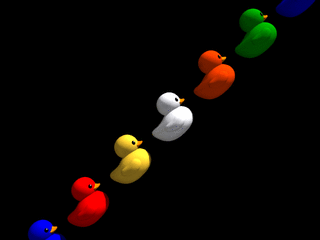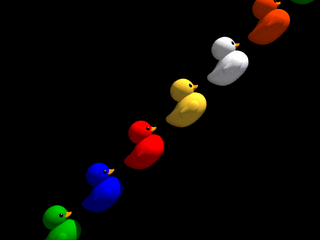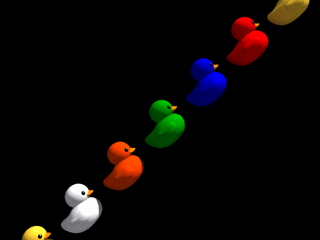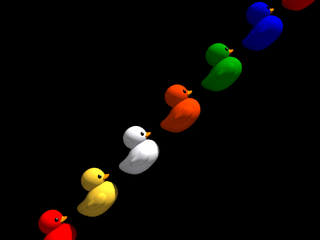
Disons-le tout net : le monde parallèle qui nous occupe ne tolère aucun relief ! Quelle que soit l'inclinaison de la pente empruntée par une file de canards, cette file se retrouve sur un sol parfaitement plat dans une photo-finish ! Cela est dû au fait que pour une pente quelconque, chaque canard de la file passe à la même hauteur que les autres derrière la fente d'obturation. Le monde comme représentation dans la phénoménologie d'une fente est définitivement despotique...
Fort heureusement cela n'est pas tout à fait vrai : premièrement, lorsque la pente est à 90 degrés (certes difficile à grimper !) on obtient une inclinaison non nulle dans la photo-finish, fonction de la vitesse de montée des canards; notons toutefois que dans ce cas, les canards ne sont plus identifiables (ont-ils peur de montrer leur visage du fait de cette transgression ?), car seule une fine bande verticale extraite de leur image est dupliquée à hauteur croissante dans la photo-finish. Deuxièmement, nous allons voir dans la section suivante comment contrer ce régime à tendance totalitaire et obtenir de lui des pentes de n'importe quel angle, aussi bien que des canards qui se regardent !
Photos-finish animées
La photographie mesure l'espace sur une infime épaisseur de temps, la photo-finish mesure le mouvement sur une infime épaisseur d'espace. La critique d'art Shana Nys Dambrot voit dans cette dualité position / mouvement une illustration du principe d'incertitude d'Heisenberg[7].
De même qu'il est impossible, avec une seule photographie, de connaître la position des objets de l'espace avant et après l'instant de mesure, il est impossible, avec une seule photo-finish, de connaître le mouvement des objets de l'espace à gauche et à droite du lieu de mesure. Et de même que plusieurs photographies prises à des instants contigus permettent de compléter la représentation de l'espace sur une durée plus grande, plusieurs photos-finish prises à travers des fentes contigues permettent de compléter la représentation des mouvements sur un espace plus large.
Afin de préciser les choses, considérons une séquence vidéo de N images numériques de définition LxH pixels chacune. Une photo-finish numérique peut être obtenue en mettant bout-à-bout la colonne centrale (de définition 1xH) de ces N images, formant une image de définition NxH. Mais plutôt que d'utiliser la colonne centrale de chaque image, nous pouvons très bien utiliser la première colonne, ou la deuxième, etc. jusqu'à la colonne L. Nous obtenons alors une séquence de L photos-finish de définition NxH chacune. J'appelle séquence duale la séquence ainsi obtenue.
 |  |
 |  |
La séquence initiale comporte Nx(LxH) pixels, la séquence duale en comporte Lx(NxH), ce qui est identique. Les deux séquences sont porteuses de la même information et le processus de transformation d'une séquence vidéo en une photo-finish animée est réversible. Le processus qui permet de reconstituer la séquence initiale à partir de la séquence duale est d'ailleurs le même que celui qui permet d'obtenir la séquence duale à partir de la séquence initiale. La séquence duale d'une séquence duale est la séquence initiale[8] !
Les animations duales de toutes les animations synthétiques présentées sur cette page sont affichées en troisième colonne des deux pages visibles dans une fenêtre à part. La dualité permet en particulier de savoir quels mouvements doivent être observés pour obtenir une photo-finish particulière. Ainsi, les photos-finish des animations ci-contre font apparaître des images apparemment "normales" présentant des configurations spatiales que l'on croyait impossibles. Elles sont en fait les empreintes des mouvements observables dans les photos-finish animées. Pour obtenir un manège à canards, il faut donc deux files de canards avançant en sens contraire, dont une à reculons ! Pour obtenir une file de canards inclinée (un escalator), il faut une file de canards horizontale montant en diagonal (un téléphérique).
Photo-finish et interprétation artistique
Pour qui n'a jamais vu
de photo-finish, une série de tableaux telle que la Montée de
Saint-Paul peut faire penser que les "déformations" singulières
observées au niveau des personnages sont le fruit de l'imagination
débordante d'un artiste atypique. Et comme ces formes sont gouvernées
par les lois d'une certaine physique, il émanera d'un ensemble de
tableaux réalisés selon la même technique, une cohérence
indéfinissable derrière laquelle d'aucuns ne manqueront pas de déceler
la "patte de l'artiste". Or, si patte il y a
derrière les formes platoniciennes que j'ai eu l'honneur de présenter dans cet article, il ne peut s'agir que de celle de l'Esprit
universel lui-même, Grand Démiurge du Temps et de l'Espace !
Pour autant, si les formes visibles dans une photo-finish ont le statut de réalité objective, le thème abordé, la composition de l'œuvre (choix des sujets et de leurs mouvements, cadrage dans l'espace et dans le temps), la technique utilisée etc. sont du seul ressort de l'artiste. Et il suffit de comparer les travaux de deux artistes photographes contemporains tels que Michael Golembewski ou Jay Mark Johnson pour constater que la photo-finish est au moins aussi riche que la photographie "classique" en terme de potentialité d'expression.
Notes et références
|
